개요
https://www.acmicpc.net/problem/1007
1007번: 벡터 매칭
평면 상에 N개의 점이 찍혀있고, 그 점을 집합 P라고 하자. 집합 P의 벡터 매칭은 벡터의 집합인데, 모든 벡터는 집합 P의 한 점에서 시작해서, 또 다른 점에서 끝나는 벡터의 집합이다. 또, P에 속
www.acmicpc.net
문제는 다음과 같습니다.
- 평면에 점들의 집합인 P가 있고 여기에는 N개의 좌표가 있다, N은 짝수이다.
- 집합 P에서 N개의 벡터를 만들 수 있다, 즉 벡터는 N/2개이다.
- P에서 나오는 벡터들의 합 중 최솟값을 출력해라.
이 문제를 풀려면 우선
🔍벡터의 합은 어떻게 구하는가?
벡터의 값은 끝점 - 시작점으로 구할 수 있습니다.
벡터 v1는 x1, y2에서 x2, y2로 향한다
v1 = (x2-x1, y2-y1)벡터 v2는 x3,y3에서 x4, y4로 향한다.
v2 = (x4-x3, y4-y3)
합은 x좌표들의 값, y좌표들의 값을 다 구하는 걸로 구할 수 있습니다.
v1 + v2 = (x2+x4 -x1-x3, y2+y4 -y1-y3)즉 v1+v2+v3+....+vn 까지의 합이 가장 적게 나오게 벡터가 매칭되는 경우의 수를 찾는 게 문제의 핵심입니다.
🔍위 공식의 성질이 뭘까
위 공식을 유심히 보면 어차피 다 +하거나 -하니 더하는 끼리의 순서는 상관이 없다는 걸 알 수 있습니다.
즉 끝점이 동일하다면 시작점이 어디 끝점을 향하든 이들을 더한 값은 동일하다는 걸 알 수 있습니다.
이를 그림으로 증명하면 아래와 같습니다.
x자로 교차하는 벡터를 가질 경우 빨간색 벡터를 구할 수 있습니다.
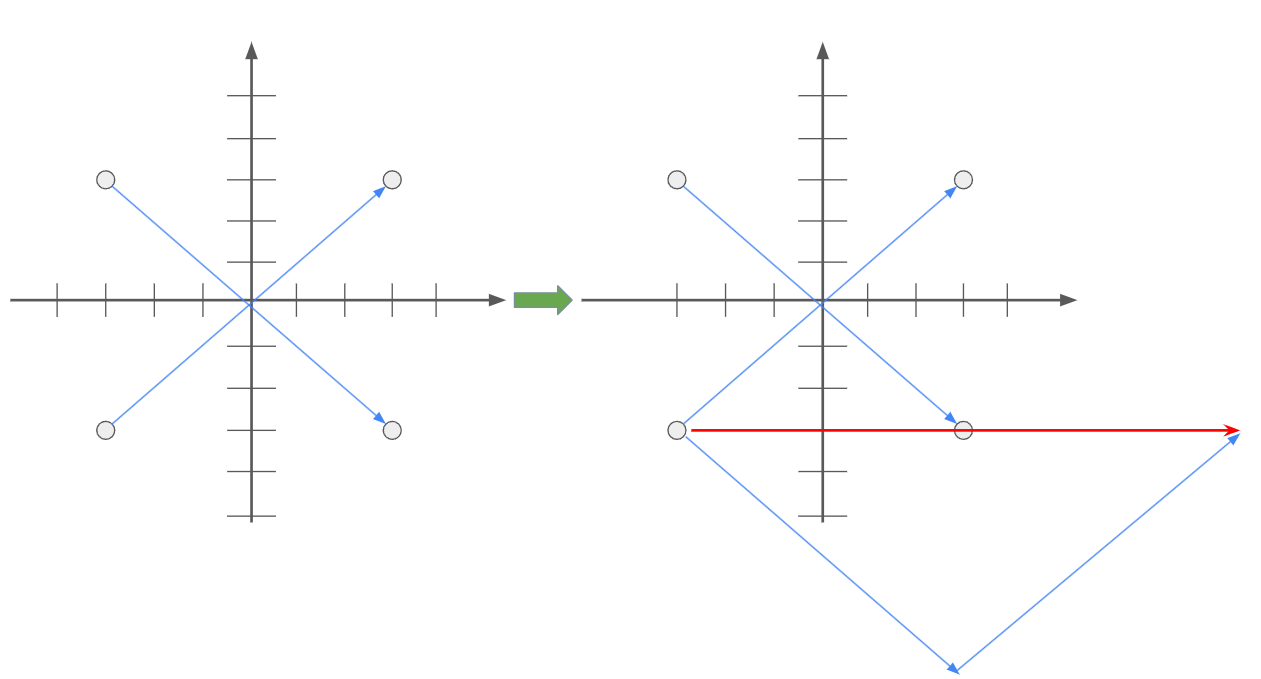
평행하는 벡터를 가질 경우 아래 처럼의 빨간색 벡터가 나옵니다
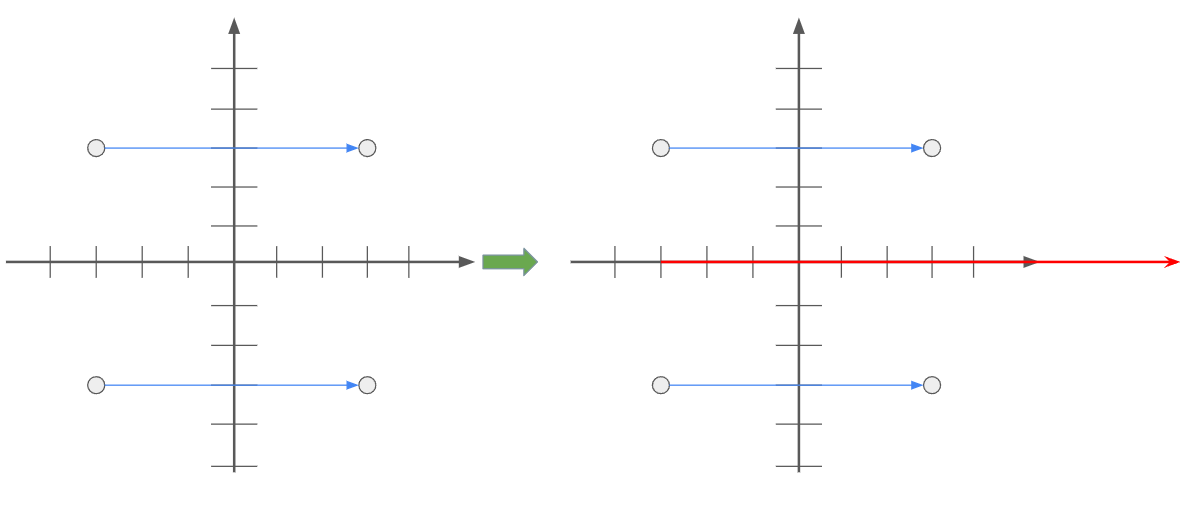
벡터에서는 이 두 값을 일치하다고 봅니다, 그래서 합의 값이 같죠
그래서 끝점이 정해졌다면 고정된 합의 값이 나옵니다.
🔍그러면 어떻게 끝점의 경우의 수를 구할래?
하나의 값이 두 개의 값만 나타낼 수 있는 좌표의 개수만큼 수열이 필요하다
이걸로는 2진수라고 컴퓨터에서 가장 유명한 친구가 있죠
만약에 좌표가 4개일 때 끝점을 구분하기 위해 1이 끝점이라 할 경우
=> 0011, 0101, 0110, 1001, 1010, 1100
이런 식으로 경우의 수를 구할 수 있습니다!
또한 좌표 값이 4라 가정 후 1를 4번 왼쪽 쉬프트 연산을 한 2진수 10000 아래의 값들로
반복문을 돌리면 위 경우의 수를 다 얻을 수 있습니다.
🔍그래도 결국 나온 값은 x,y 좌표잖아 최소의 합은 하나인데?
이미 구한 x, y는 벡터들의 합입니다.
이걸 제곱하여 더한 후 제곱근을 하면 벡터의 합이 나옵니다.
sumX, sumY가 아래 공식을 구한 x 좌표, y좌표이라고 할 때
v1 + v2 = (x2+x4 -x1-x3, y2+y4 -y1-y3)거리는 다음 코드로 구할 수 있습니다.
distance := math.Sqrt(float64(sumX*sumX + sumY*sumY))
코드
package main
import (
"fmt"
"math"
"math/bits"
)
// Point : 좌표 구조체
type Point struct {
x, y int
}
// solve : 좌표들로 만들 수 있는 벡터의 합들에서 최소값을 구하는 함수
func solve(points []Point, n int) float64 {
// 최소값을 구하기 위해 무한대(가장 큰)수로 초기화
minDistance := math.Inf(1)
// points의 길이만큼 커지는 2의 거듭제곱, 2^n
number := (1 << uint(len(points)))
// 서브넷으로 절반을 나눈다 개념인듯
for subset := 0; subset < number; subset++ {
// subset을 2진수로 변환했을 때 1의 개수
count := bits.OnesCount(uint(subset))
// count가 n/2와 같다면 => 딱 절반을 나누는 경우의 수
if count == n/2 {
sumX, sumY := 0, 0
for i, p := range points {
// 좌표 4개면 0000 ~ 1111까지 16가지 경우의 수에서
// 0011, 0101, 0110, 1001, 1010, 1100 이런식으로
// 2개씩 묶어서 끝점과 시작점을 나누는 것
// if) i번째 비트가 1이면 끝점으로 생각하고, else) 0이면 시작점으로 생각
// 끝점은 더하고
if subset&(1<<uint(i)) != 0 {
sumX += p.x
sumY += p.y
} else {
// 시작점은 뺀다
sumX -= p.x
sumY -= p.y
}
}
// 두 점사이의 거리를
// 피타고라스로 계산
distance := math.Sqrt(float64(sumX*sumX + sumY*sumY))
// 최소값 갱신
if distance < minDistance {
minDistance = distance
}
}
}
return minDistance
}
func main() {
// 테스트 케이스 입력
var testCase int
fmt.Scanln(&testCase)
for i := 0; i < testCase; i++ {
// 점의 개수 입력
var number int
fmt.Scanln(&number)
// points 좌표 배열 선언
points := make([]Point, number)
for j := 0; j < number; j++ {
// 좌표 입력
fmt.Scanln(&points[j].x, &points[j].y)
}
fmt.Println(solve(points, number))
}
}
이번 문제는 수학 지식이 많아 설명하기 어려웠습니다.
대신 2진수로 경우의 수를 구한다는 개념이 신박합니다
'Go Lang > Algorithm' 카테고리의 다른 글
| [GoLang] 백준 1012번, 유기농 배추 풀어보기 (0) | 2024.05.13 |
|---|---|
| [GoLang] 백준 1019번, 책 페이지 (0) | 2024.02.22 |
| [GoLang] 백준 1005번, ACM Craft(위상 정렬) (1) | 2024.02.11 |
| [GoLang] 백준 1004번, 어린 왕자(피타고라스 정리) (1) | 2024.02.09 |
| [GoLang] 백준 2252번, 줄 세우기(위상 정렬) (0) | 2024.02.06 |
