개요
https://www.acmicpc.net/problem/1004
1004번: 어린 왕자
입력의 첫 줄에는 테스트 케이스의 개수 T가 주어진다. 그 다음 줄부터 각각의 테스트케이스에 대해 첫째 줄에 출발점 (x1, y1)과 도착점 (x2, y2)이 주어진다. 두 번째 줄에는 행성계의 개수 n이 주
www.acmicpc.net
처음 이 문제를 보고 골치가 아플 것 같았는데 유심히 보니
정답률이 높아서 계속 문제를 읽었더니
이 문제는 낚시가 있어서 이 부분만 안 속으면 매우 쉽습니다.
문제가 아래처럼 주어진다면
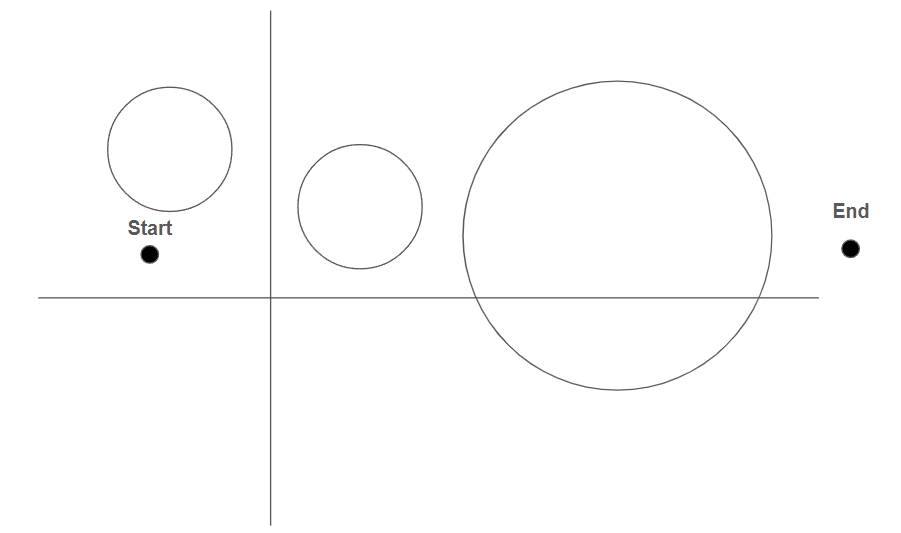
뭔가 아래처럼원 사이를 구불구불 지나가야 제대로 푼 거 같은 기분이 들지만
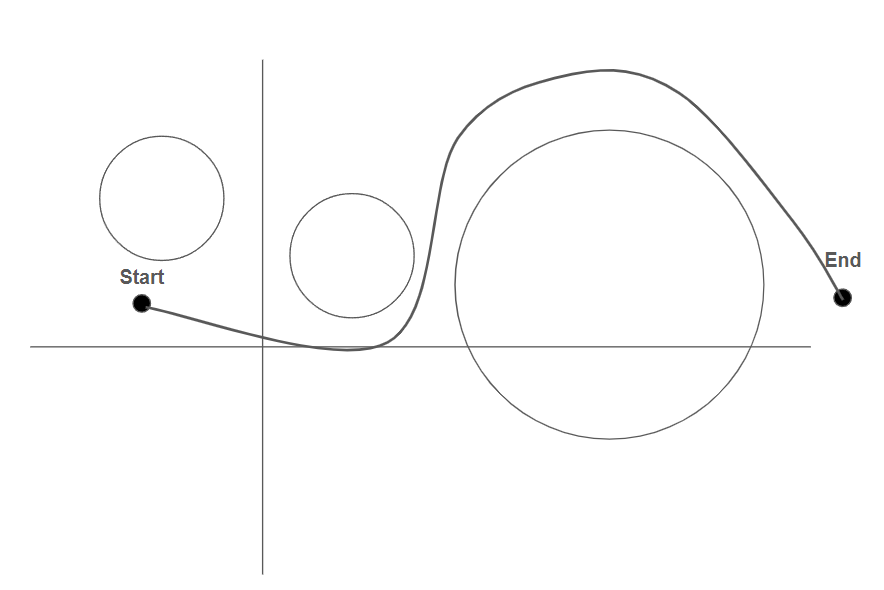
사실 아래처럼 간단하게 뒤로 돌아간다는 경우의 수가 항상 존재합니다!
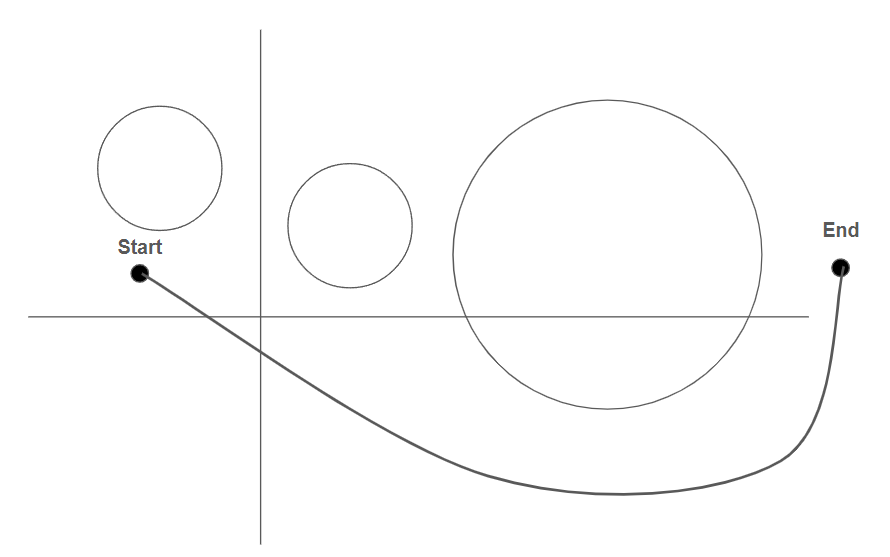
즉 문제에서 말한 행성의 경계에 진입/이탈하는 경우는 시작점과 끝점이 행성의 경계에 포함되는 경우 밖에 없게 됩니다.
그러면 포함 여부는 어떻게 아느냐 하면 간단하게 피타고라스 정리를 생각하면 됩니다.
아래 이미지처럼 비교하려는 점과 원의 중심의 거리로 만들 수 있는 높이와 가로를 만들 수 있습니다.
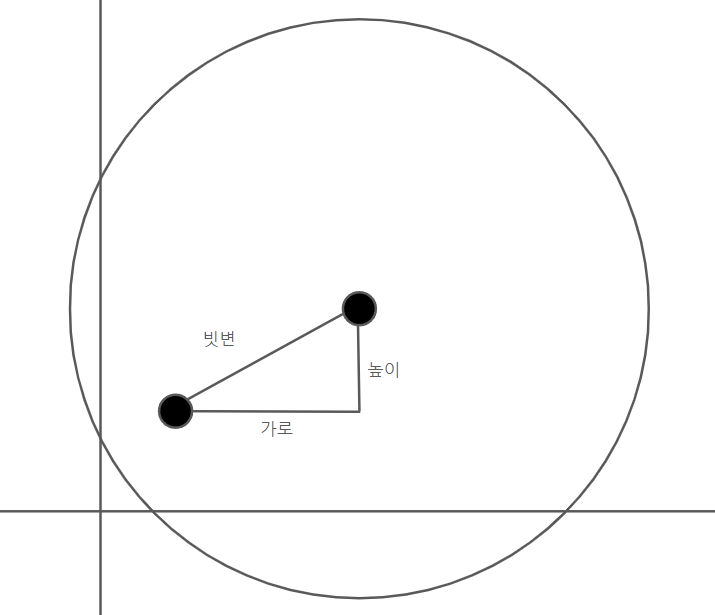
가로의 제곱 + 높이의 제곱 = 빗변의 제곱입니다.
이제 문제에 이걸 대입했을 때 가로의 제곱 + 높이의 제곱 < 원의 반지름의 제곱이 성립한다면
그 점은 원의 경계 안에 포함된다는 의미가 되죠
문제에서 출발점이나 도착점이 행성계 경계에 걸쳐진 경우 역시 입력으로 주어지지 않는다.로 알려줬기에 <로 비교하시면 됩니다.
코드
package main
import (
"bufio"
"fmt"
"os"
)
func main() {
reader := bufio.NewReader(os.Stdin)
var testCases int
// 테스트 케이스 입력
fmt.Fscanln(reader, &testCases)
for i := 0; i < testCases; i++ {
// 시작점, 도착점 입력
var x1, y1, x2, y2 int
var result int
fmt.Fscanln(reader, &x1, &y1, &x2, &y2)
// 행성 개수
var n int
fmt.Fscanln(reader, &n)
for j := 0; j < n; j++ {
// 행성 좌표, 반지름 입력
var cx, cy, r int
fmt.Fscanln(reader, &cx, &cy, &r)
// 단 둘이 같은 행성계 경계에 있으면 일탈을 안하므로
// 한쪽은 참 한쪽은 거짓이 나와야 함
if isCenterIn(x1, y1, cx, cy, r) != isCenterIn(x2, y2, cx, cy, r) {
result++
}
}
fmt.Println(result)
}
}
// isCenterIn : 행성의 중심이 사각형 안에 있는지 확인
// x, y : 비교 좌표
// cx, cy : 행성 좌표
// r : 행성 반지름
func isCenterIn(x, y, cx, cy, r int) bool {
// 값의 차가 마이너스여도 제곱이므로 상관 없음
return (x-cx)*(x-cx)+(y-cy)*(y-cy) < r*r
}'Go Lang > Algorithm' 카테고리의 다른 글
| [GoLang] 백준 1007번, 벡터 매칭 (1) | 2024.02.18 |
|---|---|
| [GoLang] 백준 1005번, ACM Craft(위상 정렬) (1) | 2024.02.11 |
| [GoLang] 백준 2252번, 줄 세우기(위상 정렬) (0) | 2024.02.06 |
| [GoLang] 백준 1009번, 분산처리(제곱 수의 일의 자리) (1) | 2024.02.04 |
| [GoLang] 백준 1260번, DFS와 BFS (1) | 2024.01.29 |
개요
https://www.acmicpc.net/problem/1004
1004번: 어린 왕자
입력의 첫 줄에는 테스트 케이스의 개수 T가 주어진다. 그 다음 줄부터 각각의 테스트케이스에 대해 첫째 줄에 출발점 (x1, y1)과 도착점 (x2, y2)이 주어진다. 두 번째 줄에는 행성계의 개수 n이 주
www.acmicpc.net
처음 이 문제를 보고 골치가 아플 것 같았는데 유심히 보니
정답률이 높아서 계속 문제를 읽었더니
이 문제는 낚시가 있어서 이 부분만 안 속으면 매우 쉽습니다.
문제가 아래처럼 주어진다면

뭔가 아래처럼원 사이를 구불구불 지나가야 제대로 푼 거 같은 기분이 들지만

사실 아래처럼 간단하게 뒤로 돌아간다는 경우의 수가 항상 존재합니다!

즉 문제에서 말한 행성의 경계에 진입/이탈하는 경우는 시작점과 끝점이 행성의 경계에 포함되는 경우 밖에 없게 됩니다.
그러면 포함 여부는 어떻게 아느냐 하면 간단하게 피타고라스 정리를 생각하면 됩니다.
아래 이미지처럼 비교하려는 점과 원의 중심의 거리로 만들 수 있는 높이와 가로를 만들 수 있습니다.

가로의 제곱 + 높이의 제곱 = 빗변의 제곱입니다.
이제 문제에 이걸 대입했을 때 가로의 제곱 + 높이의 제곱 < 원의 반지름의 제곱이 성립한다면
그 점은 원의 경계 안에 포함된다는 의미가 되죠
문제에서 출발점이나 도착점이 행성계 경계에 걸쳐진 경우 역시 입력으로 주어지지 않는다.로 알려줬기에 <로 비교하시면 됩니다.
코드
package main
import (
"bufio"
"fmt"
"os"
)
func main() {
reader := bufio.NewReader(os.Stdin)
var testCases int
// 테스트 케이스 입력
fmt.Fscanln(reader, &testCases)
for i := 0; i < testCases; i++ {
// 시작점, 도착점 입력
var x1, y1, x2, y2 int
var result int
fmt.Fscanln(reader, &x1, &y1, &x2, &y2)
// 행성 개수
var n int
fmt.Fscanln(reader, &n)
for j := 0; j < n; j++ {
// 행성 좌표, 반지름 입력
var cx, cy, r int
fmt.Fscanln(reader, &cx, &cy, &r)
// 단 둘이 같은 행성계 경계에 있으면 일탈을 안하므로
// 한쪽은 참 한쪽은 거짓이 나와야 함
if isCenterIn(x1, y1, cx, cy, r) != isCenterIn(x2, y2, cx, cy, r) {
result++
}
}
fmt.Println(result)
}
}
// isCenterIn : 행성의 중심이 사각형 안에 있는지 확인
// x, y : 비교 좌표
// cx, cy : 행성 좌표
// r : 행성 반지름
func isCenterIn(x, y, cx, cy, r int) bool {
// 값의 차가 마이너스여도 제곱이므로 상관 없음
return (x-cx)*(x-cx)+(y-cy)*(y-cy) < r*r
}'Go Lang > Algorithm' 카테고리의 다른 글
| [GoLang] 백준 1007번, 벡터 매칭 (1) | 2024.02.18 |
|---|---|
| [GoLang] 백준 1005번, ACM Craft(위상 정렬) (1) | 2024.02.11 |
| [GoLang] 백준 2252번, 줄 세우기(위상 정렬) (0) | 2024.02.06 |
| [GoLang] 백준 1009번, 분산처리(제곱 수의 일의 자리) (1) | 2024.02.04 |
| [GoLang] 백준 1260번, DFS와 BFS (1) | 2024.01.29 |
